Samuel J Gurr, PhD

Metabolic scaling bfactor

by Samuel J Gurr PhD 1 min read

Objective and summary:

When possible, it is critical to normalize physiological rates allometrically, as they are often proportional to boy mass.

from Bayne text

Of all the factors affecting metabolic rate, body size is fundamental (Schmidt-Nielsen, 1984). The earliest studies (scientific interest in the topic goes back to the 19th century) resolved that metabolic rates across different species are proportional to body mass (M) raised to a power b, expressed in the allometric equation: M_O2∝aMb, for which the linear transformation is log10 M_O2 1⁄4 log10aþð Þ b log10M ; b is the scaling exponent (the regression slope) and a is a proportionality coefficient (the regression intercept, or metabolic rate per unit mass). Early attempts to evaluate the exponent b argued that metabolic rate is proportional to surface area and therefore to M2/3.

Summary…

  • EQ.1 Data input: log10_M_O2 = log10_a + (b.factor * log10_Mass)

  • EQ.2 Resulting fit: [ln(VO2])] = ln(a) + b*(ln(TDW))

    • Assuming… M_O2 ∝ a*Mass^(b.factor) OR y ∝ m(x)^b.factor

Lets do it

(1) Regress the log10(VO2) against log10(TDW)

  • view figure below

  • top == contains all day recorded thus far that has TDW recorded

  • bottom == parsed by pCO2 treatment

    • NOTE: smaller individuals not included as fragility and size confounded accurate dissectoin and estimation of TDW

bfactor_log_plots

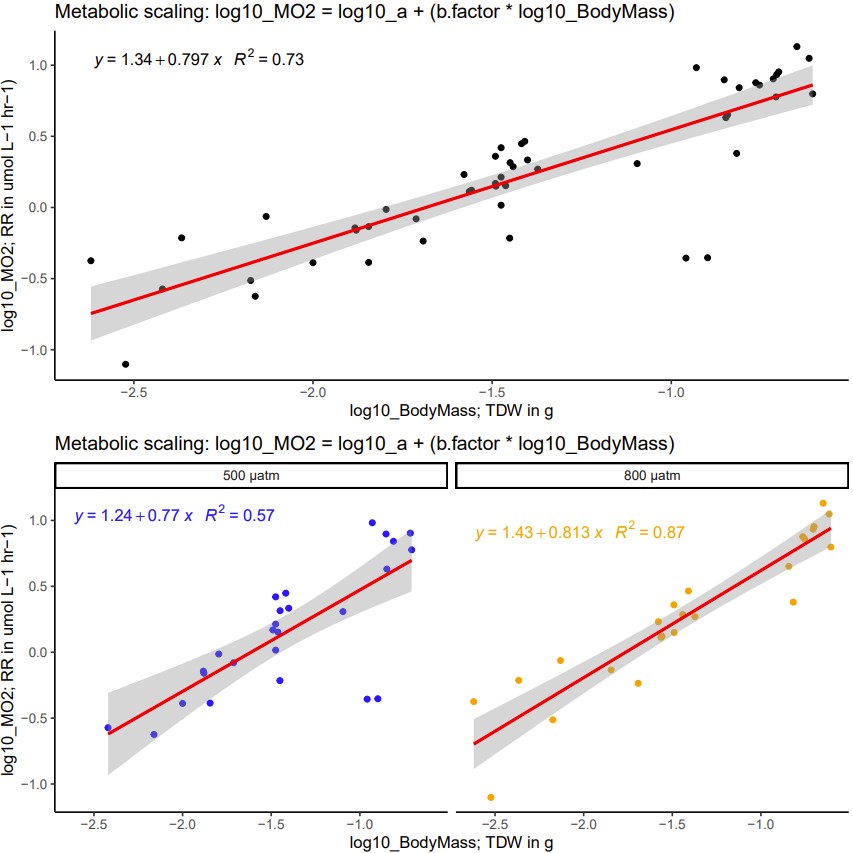
there are two strong outliers, omitted them below..

(2) Regress the log10(VO2) against log10(TDW) with outlier(s) removed

  • we now have a consistent b factor for all data, omitting the outliers reduced the difference between pCO2 treatment

bfactor_log_plots_OM

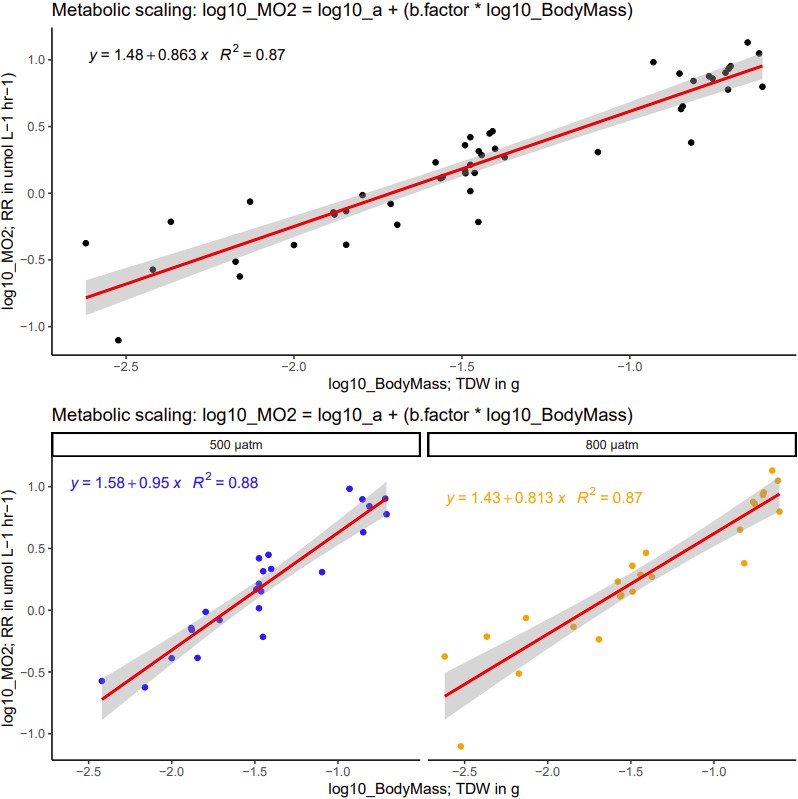
(3) Integrate and compare use of b factor

  • b factor = 0.863 (outliers omitted above)

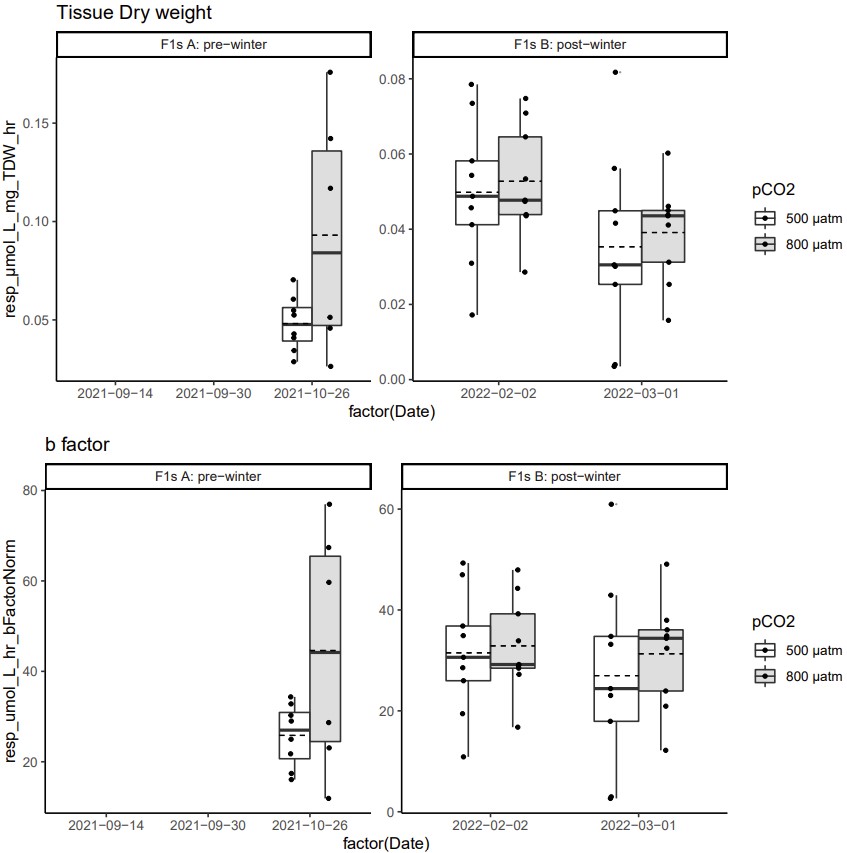
  • top == boxplots below for the size corrected metabolic rates (umol O2 L-1 hr-1 gTDW-1)

  • bottom == boxplots for metabolic rates normalized allometrically (umol O2 L-1 hr-1 ^ bfactor)

bfactor_boxplots